利用 Grasshopper 绘制冯·卡门曲线

前言

冯·卡门曲线在航天中被广泛应用于整流罩等部件，以降低空气阻力。在设计火箭等纸模型时，难免会和它打交道。由于冯·卡门曲线属于非线性曲线，由它绕转而成的曲面也是一个不可展开的曲面。

在纸模型设计中，这类部件往往需要被拆分为多个可展开曲面（比如拆分成若干个圆台与圆锥）。手动建模时，可以依照肉眼的直觉直接在不同高度画圆，然后放样。但这种做法不利于后期的调整。如果要建的模型不止一个，那么建模者也不得不进行重复劳动。此外，用这种方法画出的截面往往不够平滑，很容易让人产生违和感。

于是，我决定研究一下如何在 Grasshopper 中做出带有冯·卡门曲线的整流罩截面曲线。

思路

冯·卡门曲线的公式为

$\theta=\arccos(1-\frac{2x}{L})\\ r(\theta)=\frac{R}{\sqrt{\pi}}\sqrt{\theta-\frac{\sin 2\theta}{2}}$

虽然看起来绘制这个曲线非常简单，但问题在于大部分火箭的整流罩截面曲线都不是完整的冯·卡门曲线——整流罩顶部往往是球形的，而冯·卡门曲线绕转出的锥体必有尖端。当球径较小的时候视觉效果还行，球径较大时，曲线和实物的差距就非常大了。

为了得到比较好的效果，势必要将整流罩曲线分为两段——冯·卡门曲线段与圆弧段。

于是可以得到大概思路：

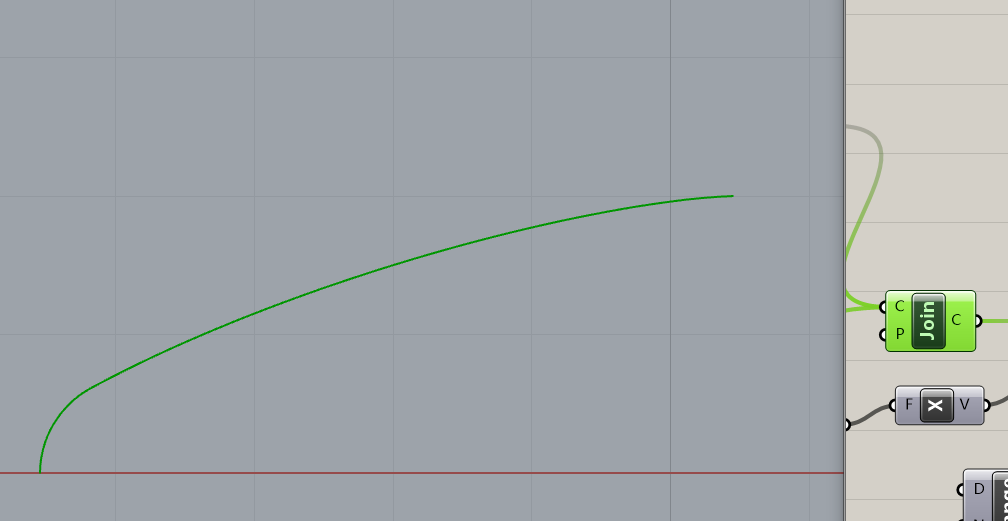
绘制冯·卡门曲线
取断点，求断点处斜率
根据斜率计算圆弧大小与位置

但是这种方式存在一个问题：无法较为准确地得到高度一定的曲线，需要进行调参。

所以需要在以上步骤的基础上加上：

计算总长
根据总长自动修正参数（L）

实现

利用原生的 Grasshopper 显然是难以实现自动修正参数的——这需要循环语句，所以这时便需要使用 Python 了。

虽然在折腾这个功能前我还没接触过 Python，但好在这个问题本身并不复杂，也不需要进行什么优化。~~大力出奇迹~~

__author__ = "FZDSL"
__version__ = "2022.01.14"

import rhinoscriptsyntax as rs
import math

L=float(Length)
R=float(Radius)
i=float(interrupt)

def voncarman(x):
    global L,R
    theta=math.acos(1-(2*x/L))
    m=(R/math.sqrt(math.pi))*math.sqrt(theta-(math.sin(2*theta)/2))
    return m

def derivation(y):
    global deltax,L,deltaxsub,deltaxadd,Length,vy,vz,dist
    z=y+0.001
    vy=voncarman(y)
    vz=voncarman(z)
    dist=(vz-vy)*1000
    deltaxsub=vy*dist
    deltaxadd=deltaxsub/math.sin(math.atan(dist))
    deltax=abs((L-Length)-(i-(deltaxadd-deltaxsub)))
    return

derivation(i)


while(deltax>0.001):
    L=L+0.001
    derivation(i)


r=L
a=i+deltaxsub-deltaxadd